Mastering Bar Models in Mathematics
Explore the power of bar modelling in mathematics, its impact on problem-solving, and how it enhances primary students' math mastery.


Explore the power of bar modelling in mathematics, its impact on problem-solving, and how it enhances primary students' math mastery.
Mathematics can often seem daunting, but visual tools like bar models can transform the way students understand numbers. By translating complex problems into easily digestible visuals, these models provide clarity and facilitate deeper mathematical comprehension.
Bar models serve as powerful representations of mathematical concepts, allowing learners to visualize relationships between numbers. They are particularly significant in helping students grasp operations like addition, subtraction, multiplication, and division through concrete illustrations.
This article will explore the importance of bar models in math education, effective strategies for introducing them to students, common misconceptions to address, and their real-world applications. By mastering bar models, both educators and students can enhance their mathematical skills and foster a long-lasting understanding of the subject.
Bar models are crucial because they provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts. They help students visualize relationships between numbers and understand operations like addition, subtraction, multiplication, and division more deeply. This visual approach is particularly effective for students who struggle with traditional abstract number concepts.
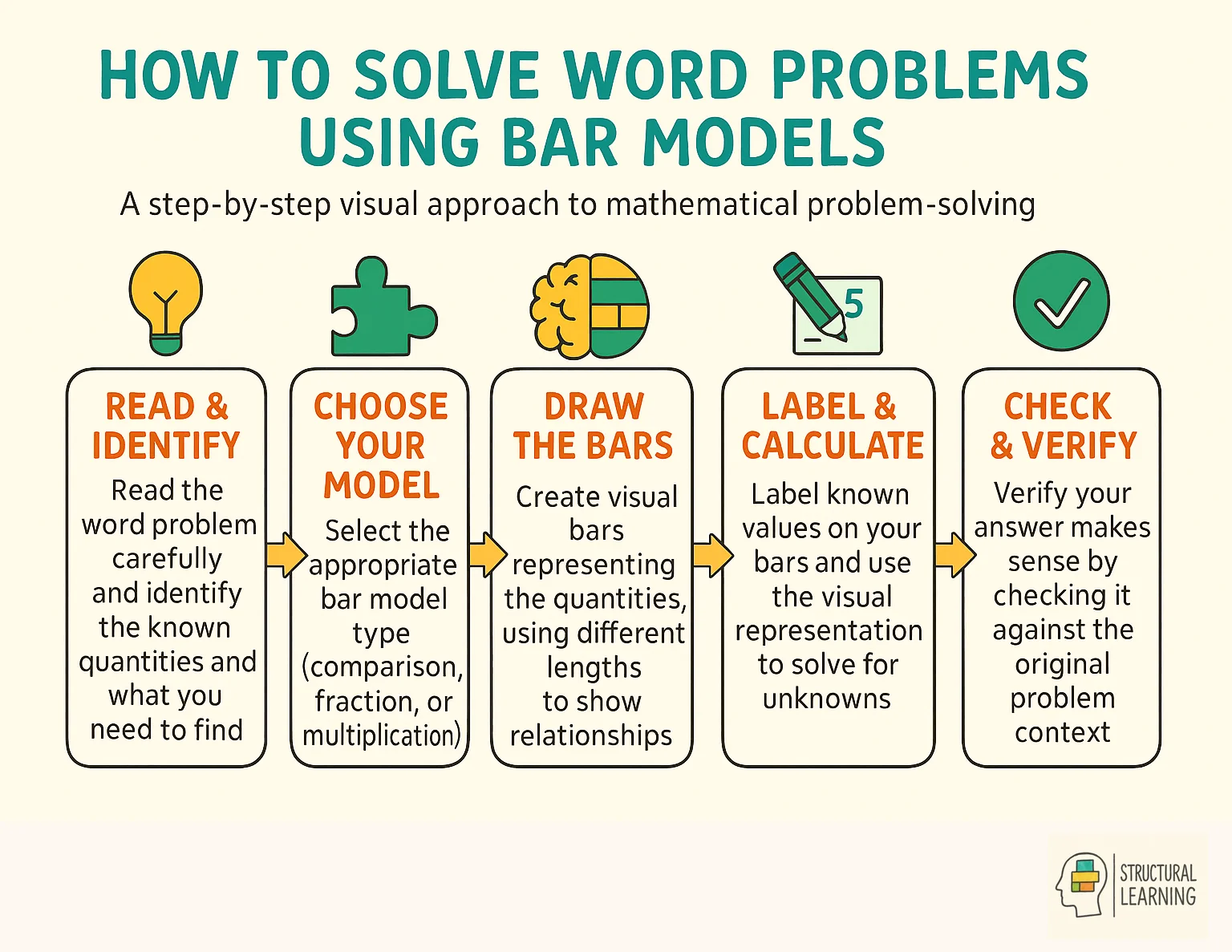
Bar models are powerful tools in math education, offering visual representations that enhance a student's conceptual understanding. They serve as a bridge, connecting concrete objects with abstract mathematical concepts. By doing so, they help students grasp math operations like addition, subtraction, multiplication, and division more deeply.
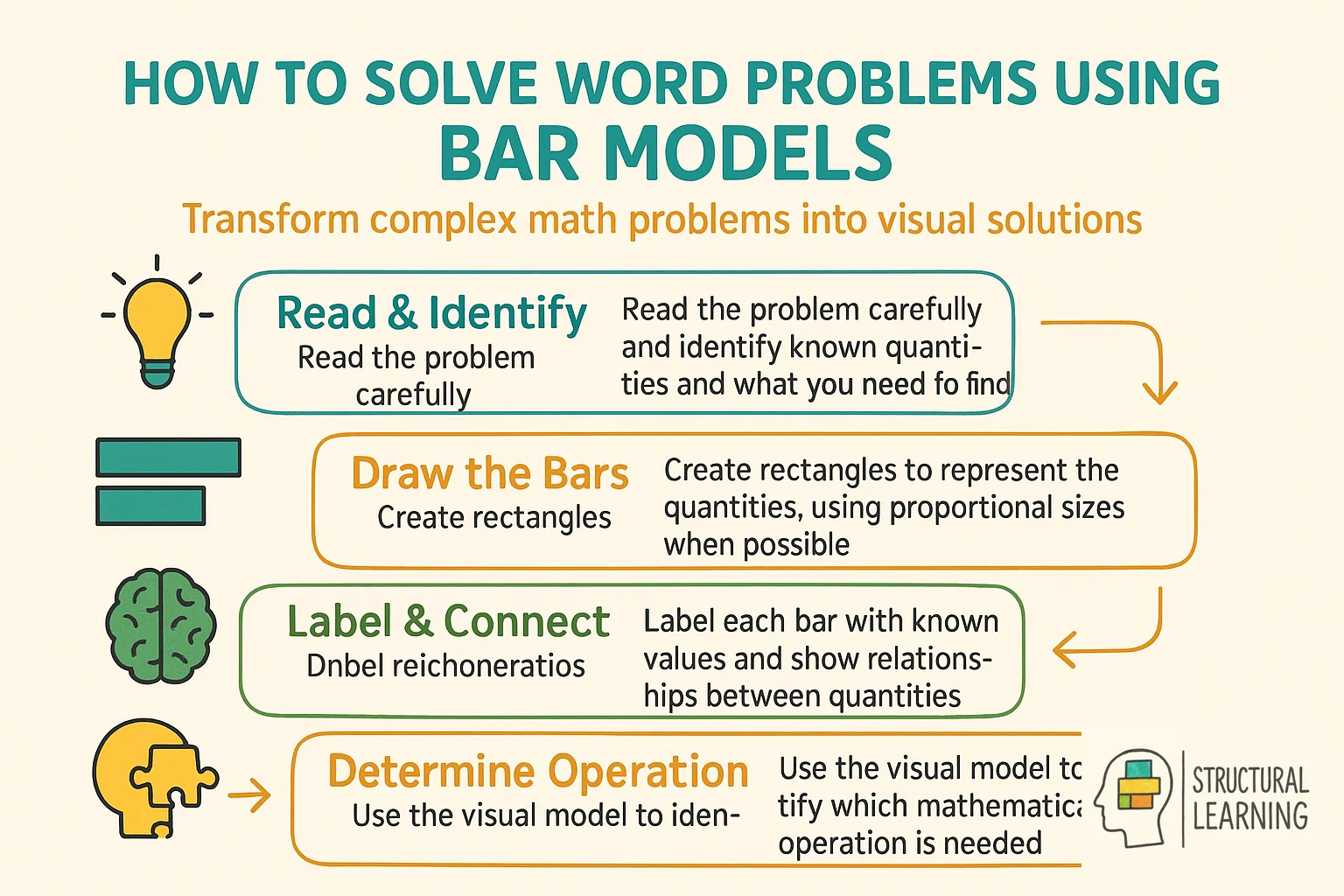
Bar models come in various types, such as comparison models and fraction bar models, catering to different mathematical concepts and operations. These pictorial diagrams enable students to visualize complex problems and compare different quantities through bar model examples.
| Bar Model Types | Usage |
|---|---|
| Comparison Bar Models | Used for comparing quantities |
| Fraction Bar Models | Helps in understanding fractions |
| Bar Model Multiplication | Visualizes multiplication equations |
In conclusion, bar modelling is a versatile tool that can significantly impact pupils' understanding, boosting their confidence in math.
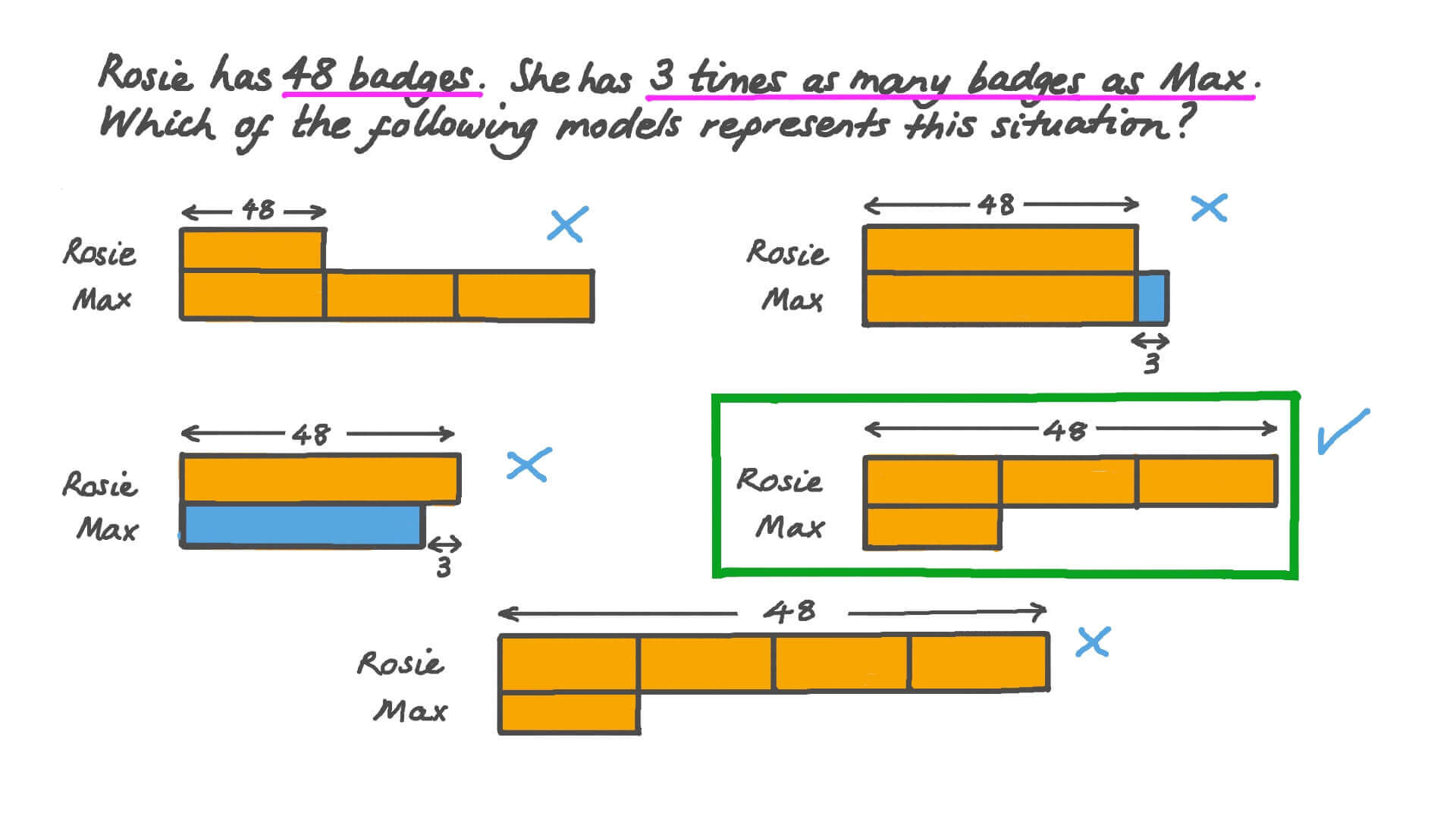
Bar models are visual representations using rectangles to help solve arithmetic problems. They are part of the concrete, pictorial, abstract (CPA) teaching method, which aids understanding and mastery of math concepts. Bar models help students visualize relationships in a problem and determine needed operations. They do not provide answers but guide learners on the necessary calculations.
Bar models are pictorial representations that use rectangles or bars to show known and unknown quantities in math problems. They are commonly used for addition, subtraction, multiplication, and division. The size of the bars is proportional to the values they represent, making it easy to see the relationships between numbers. The bar model technique fits with the CPA approach, emphasizing visual learning before moving to abstract math notation.
Bar modelling is a powerful tool for solving word problems. It helps students visualize complex calculations and understand math concepts better. Once mastered, bar modelling can be used for various topics like ratios, volume, and fractions. It aids in creating a strong logical foundation. By using bar models across the curriculum, students can see links between different math areas, deepening their understanding.

| Bar Model Benefits | Description |
|---|---|
| Visual Problem Solving | Converts word problems into visual models |
| Enhances Understanding | Allows better grasp of complex math concepts |
| Encourages Application | Builds a framework for applying knowledge to new topics |
Students develop a stable framework for math by engaging with bar models, increasing their overall confidence and fluency.
Start by using concrete manipulatives before moving to pictorial bar representations, following the concrete-pictorial-abstract (CPA) approach. Begin with simple part-whole relationships and gradually progress to more complex problems involving multiple operations. Model the process explicitly first, then provide guided practice before allowing independent work.
Bar models are powerful tools that help students visualize mathematical relationships. They aid in building a strong conceptual understanding by allowing students to see the connections between numbers. The journey with bar models can start early, like in Kindergarten, with simple tools like Cuisenaire rods. As students progress to 1st grade, they can tackle more formal bar models. Teachers should first present the complete solution. This lets students focus on how the model demonstrates the solution rather than searching for the answer. Choosing the right type of bar model is crucial. Using an incorrect model can make problem-solving more difficult. The bar model technique is key in moving from concrete experiences to abstract thinking. This builds a student's number sense and problem-solving skills.
The bar model method provides a structured way to teach math concepts. Students learn to visualize and understand how parts of a problem are related. Using the Concrete, Pictorial, Abstract (CPA) approach, teachers guide students from using real objects to drawing bar models. Eventually, students reach abstract notations. Encourage students to draw and share different representations of the same math problem. This practice enhances their understanding and problem-solving flexibility. A consistent teaching method for bar models across schools ensures that students receive a uniform learning experience. This leads to better learning outcomes. Introducing abstract representations alongside bar models helps students move from pictorial understanding to advanced reasoning in math.

Bar models act as visual aids that reinforce a student's understanding of math concepts. They illustrate the relationships between different quantities. Bar models are part of the CPA teaching sequence. They help students move from using physical objects to pictorial representations and finally to abstract notation. By visualizing the needed calculations, bar models allow students to solve problems without giving direct answers. This enhances their problem-solving skills. Hands-on tools like foam bars and magnetic dry wipe boards create engaging learning experiences. These tools make it easier for students to grasp mathematical concepts. Bar models are versatile. They are used for various math topics, such as addition, subtraction, multiplication, and division. This makes them integral to intervention strategies in education.
Bar models can be applied to solve word problems involving all four basic operations, fractions, ratios, and proportions. They are particularly effective for comparison problems, multi-step word problems, and algebraic thinking in elementary grades. These models help students organize information visually and identify the mathematical relationships within problems.
Bar models are powerful tools for visualizing mathematical concepts. They help children develop a conceptual understanding by using a concrete > pictorial > abstract (CPA) approach. This method moves from tangible objects to visual and finally to abstract ideas. Bar models can represent all major math operations: addition, subtraction, multiplication, and division. This versatility aids students in solving various types of problems, especially multi-step ones. Bar modeling provides a strong foundation for solving equations and understanding complex concepts.
In addition, bar models help students visualize number relationships through proportional rectangles. These visual representations guide students to focus on what calculations are necessary for solving problems. As they progress, students become more confident with addition. This includes not just basic sums but also complex concepts like fractions and ratios. Bar models align with the National Curriculum, helping young learners use concrete objects and pictorial diagrams to understand addition.
Bar models support subtraction by showing how it differs from and relates to addition. They offer part-part-whole and find-the-difference models. This helps students choose the right approach for each problem. Teachers guide students through these stages, moving from tangible objects to pictorial representations. Bar models in subtraction lead students to visualize problems clearly and choose the right calculations for solutions.
For multiplication, bar models showcase the relationship between quantities as repeated addition. Students see the multiplication process by repeating the same visual unit. This makes understanding the scale of their calculations easier. Bar models help students move from concrete examples to abstract math concepts. Mastering bar model multiplication equips students to tackle more complex math challenges.
In division, bar models focus on sharing. They visually represent how division works by showing quantities being divided. For example, if Mr. Smith divides a piece of wood using a bar model, each piece depicts a part of the division process. This visual strategy helps students grasp the concept of division and apply it to different problems. The proportional nature of bar models aids in understanding the relationship between quantities divided, fostering deeper comprehension.

The Singapore Bar Model Method is a visual problem-solving approach that uses rectangular bars to represent known and unknown quantities in mathematical problems. This method emphasizes understanding the relationships between parts and wholes before applying computational procedures. It has been widely adopted internationally due to its effectiveness in developing mathematical reasoning skills.
The Singapore Bar Model Method is a teaching technique that helps students understand mathematical concepts. Rooted in the theories of educators like Bruner, Dienes, and Bishop, it focuses on mastery in mathematics. This method uses bar models to bridge the gap between concrete objects and abstract ideas. Bar models help students move from using real items to grasping abstract math concepts.
Bar models are a type of pictorial representation. They show quantities and relationships in a structured manner. When students become skilled with bar models, they can use them for various math topics. These include ratio problems, fractions, and volume problems. By using bar models, students improve their problem-solving skills.
The Singapore Bar Model Method is versatile. It can be tailored to fit different math problems. This adaptability makes it a powerful tool for developing number sense and mathematical fluency.
Bar models serve as a visual aid to help children solve math problems. They use proportional rectangles to show different values. This enhances a child's understanding of math operations.
Benefits of Bar Models:
The Singapore Math Model, or bar modeling, makes learning math progressive and comprehensive. It is a valuable resource for teachers aiming to fill individual learning gaps in students.
The part-whole method uses bar models to show how smaller quantities (parts) combine to form a larger quantity (whole). Students draw bars divided into sections representing the known parts and identify what needs to be found. This visual representation helps students understand addition and subtraction as inverse operations and builds number sense.
The part-whole method is a powerful tool in the math classroom. It involves breaking numbers into parts that together form a whole. This method is great for addition and subtraction. By using proportional bars, students can visualize how parts relate to the whole. This visual representation aids in understanding complex math topics like fractions, measurement, algebra, and ratios.
Proportionality is key in this method. All the bar models must be roughly proportional to each other to accurately represent relationships. This technique is versatile and can be applied in various mathematical operations. When students get to see the part-whole models, they develop a clearer conceptual understanding of numerical relationships.

Bar models are pictorial representations that help illustrate math concepts. They use rectangles to represent numbers. This helps students see how to solve problems without giving away the answers. Bar models follow the concrete-pictorial-abstract (CPA) teaching sequence. This means students start with real objects, move to pictures, and then to abstract concepts.
Bar models are suitable for all four basic math operations: addition, subtraction, multiplication, and division. This makes them very versatile tools for learning. They can enhance a student's ability to visualize number relationships in a problem, fostering deeper understanding. These models are especially helpful in education for reinforcing concepts. They benefit students during catch-up sessions and align well with curriculum objectives for Key Stages 1 and 2.
Teachers often rush to abstract representations without sufficient concrete and pictorial practice, causing student confusion. Another common mistake is using bar models for every type of problem, even when other strategies might be more appropriate. Additionally, failing to explicitly teach when and why to use specific bar model types can lead to procedural errors rather than conceptual understanding.
Bar modelling is a powerful tool in teaching mathematical concepts. However, several common mistakes can hinder its effectiveness.
Misunderstandings about bar models can arise if not addressed early. Here are some misconceptions teachers should avoid:
To maximize the benefits of bar modelling, consider these instructional tips:
By avoiding common mistakes, addressing misconceptions, and following effective teaching strategies, educators can enhance the impact of bar modelling in math lessons. This ensures a better conceptual understanding among students.
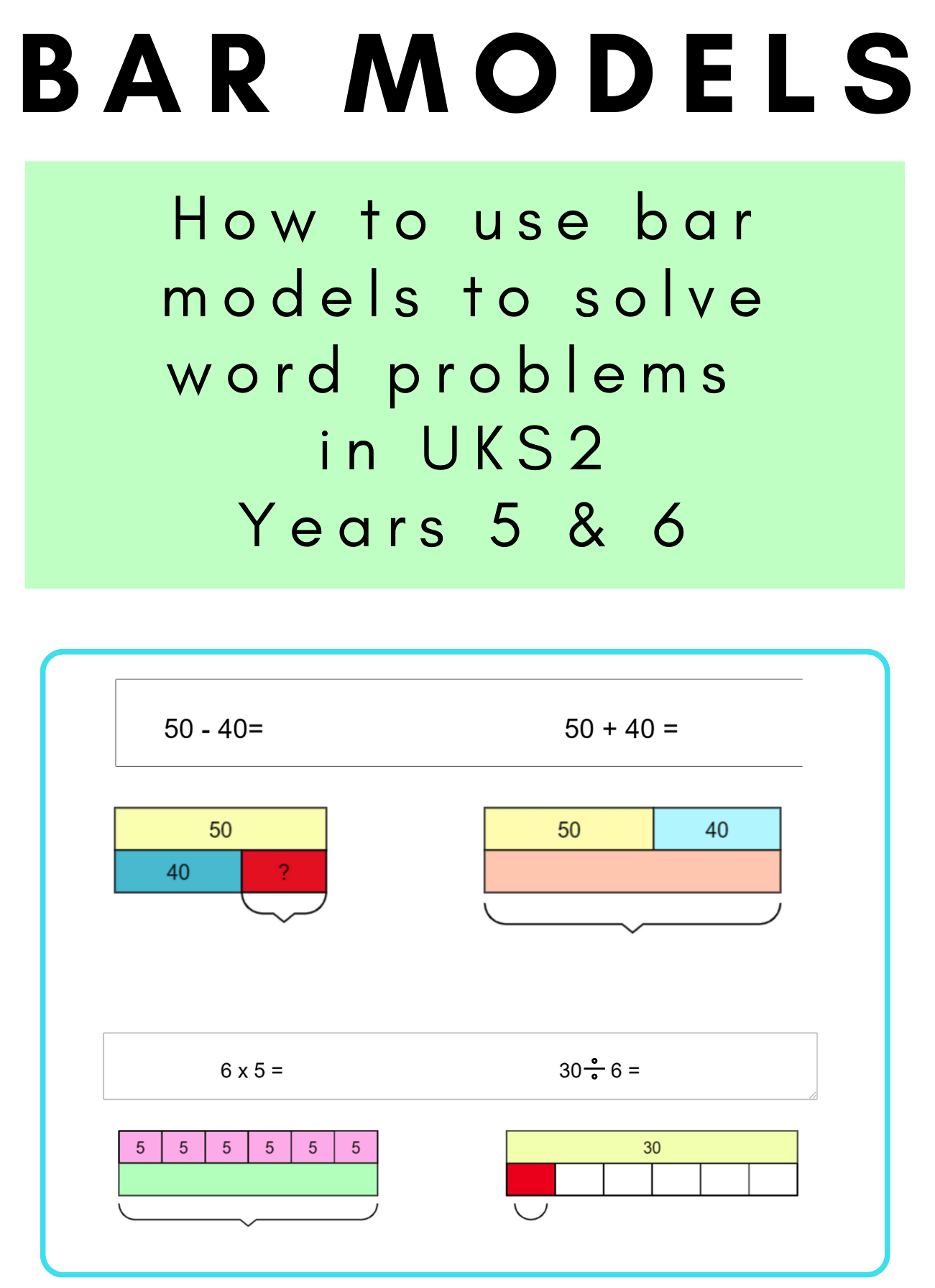
Effective practice examples start with simple comparison problems like 'Tom has 8 stickers, Jerry has 3 more than Tom, how many does Jerry have?' Progress to multi-step problems involving different operations and real-world contexts that students can relate to. Include both part-whole and comparison model types to build comprehensive problem-solving skills.
Bar modelling is a powerful tool in math lessons. It helps children understand various math operations. By using visual and pictorial representations, students can grasp complex problems. These methods are especially useful for teaching addition, subtraction, multiplication, and division. They align with the concrete > pictorial > abstract (CPA) approach, which guides students from using concrete objects to understanding abstract ideas.
To teach addition, bar models can show students how to combine quantities. For instance, if you have 6 red pencils and 4 yellow pencils, a bar model can help visualize the total number of pencils. By drawing rectangles to represent each quantity, learners can better understand what they are adding. Teachers often use worksheets that gradually increase in difficulty. This helps students solidify their understanding before creating their own problems. Bar models help connect concrete resources to abstract calculations in addition.
Subtraction can be tricky, but bar models simplify it. Consider a problem where you compare how many more football cards one person has than another. With a bar model, students can see the difference as a space between two bars. This visual representation makes it easier to find unknown quantities. Using tools like Base 10 blocks alongside bar models helps reinforce subtraction concepts. This method encourages a deep conceptual understanding and helps students move from hands-on learning to abstract problem-solving.
For multiplication, bar models show grouped sets. Imagine solving a problem where you need to multiply 4 sets of 3. A bar model illustrates this by repeating a block of 3 four times. This visualization helps students understand that multiplication is repeated addition. Complex word problems become easier as students see the operation unfold visually. By linking abstract calculations with concrete images, bar models enable a better grasp of multiplication.
Bar models are also effective for division. They represent division as sharing an amount into equal parts. For example, if Mr. Smith cuts a 36 cm piece of wood into 6 equal pieces, a bar model shows each piece as 6 cm long. By visualizing these equal shares, students can better understand division problems. This approach clarifies how larger quantities divide into smaller, equal parts. By using bar models, learners can move from concrete understanding to abstract representations in division.
These practical examples demonstrate how bar modelling resources impact pupils' learning. They fill individual learning gaps and enhance conceptual understanding in elementary math education.
Bar models help students solve everyday problems involving money, measurements, time, and quantities in cooking or shopping scenarios. They can model budget allocation, ingredient ratios in recipes, or distance and time relationships in travel problems. These applications demonstrate the practical value of mathematical thinking beyond the classroom.
Bar models are a powerful visual tool in math. They help individuals tackle various mathematical concepts without jumping straight into complex calculations. By using proportional rectangles, bar models aid in visualizing problem-solving operations such as addition, subtraction, multiplication, and division. This visual strategy is especially beneficial for understanding word problems and identifying the necessary operations to solve them. As students engage with bar models, they progress through activities of increasing complexity. This allows them to master more advanced topics, like fractions and equations. Overall, bar models enhance reasoning skills and promote problem-solving prowess.
Bar models serve as a bridge between abstract math and the real world. They help students grasp mathematical concepts and apply them in practical situations. When learners use bar models, they can visualize the relationships between problem elements. This makes it easier to perform operations like addition, subtraction, multiplication, and division. By fostering conceptual understanding, children develop a stronger number sense and fluency in math. This new skill set enables them to tackle everyday challenges with confidence, and to use mathematical skills in real-life scenarios efficiently.
The significance of bar models extends beyond the classroom. These versatile tools not only help students tackle math problems but also enhance individual learning experiences. By offering a tangible way to connect experiences with abstract reasoning, bar models lay a robust foundation in math. Their simplicity, requiring only basic materials like pencils and paper, makes them accessible resources for students in test settings. Moreover, by aiding in the conceptual understanding of math operations, bar models equip children with skills that apply to real-world contexts and other academic subjects. This approach to learning prepares students for lifelong success in any mathematical endeavor they face.
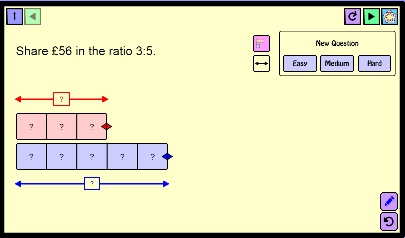
The most effective strategy is following the concrete-pictorial-abstract progression, ensuring students master each stage before advancing. Use think-alouds to model the decision-making process when choosing which type of bar model to use. Provide regular opportunities for students to explain their thinking and justify their choice of representation.
The bar model is a versatile tool that acts as a visual representation to help students understand mathematical concepts. It doesn't solve problems directly but instead reveals the mathematical structure, enhancing problem-solving skills. The bar model method is a core part of the Singapore Math approach, helping students visualize and tackle problems, from simple operations to complex word problems.
Engaging students in math can be transformative, especially when using bar models. These visual representations make complex mathematical concepts easier to understand. They help students see math problems as pictorial diagrams, allowing them to grasp abstract ideas more readily. This builds confidence and can spark a love for math in even the most reluctant learners.
One-on-one tutoring programs personalized to each student’s needs can further enhance learning. Such programs help address individual learning gaps and provide targeted support. Worksheets that incorporate bar models serve as valuable resources in these sessions. They offer structured opportunities to explore various math operations and form a solid conceptual understanding.
To cater to diverse learning styles, differentiated worksheets can be introduced. These concrete resources allow students to explore math at their own pace, enhancing engagement and participation. Here's a quick list of how bar models impact learning:
In sum, bar modelling is a versatile tool that can boost student confidence and interest in math, providing elementary math teachers with effective ways to enhance their teaching.
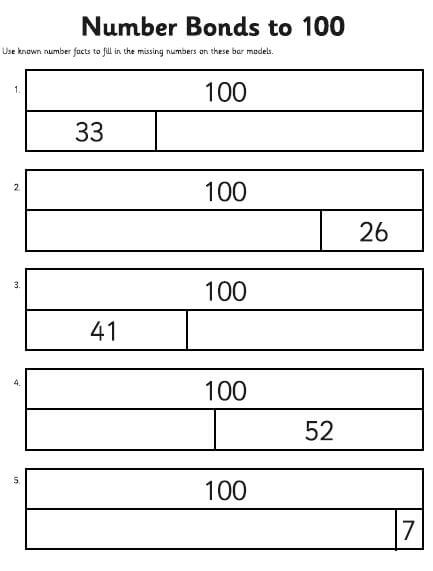
Research consistently shows that bar models improve student performance in problem-solving and mathematical reasoning, particularly for students who struggle with traditional methods. Studies indicate that students who use bar models demonstrate better understanding of mathematical relationships and transfer skills to new problem types. The visual approach has been shown to reduce cognitive load and increase engagement across diverse learner populations.
These studies highlight the effectiveness of bar modelling in enhancing students’ problem-solving skills, mathematical reasoning, and ability to transition to more abstract mathematical concepts.
1. The Effectiveness of Bar Model to Enhance HOTs in Mathematics for Year 4 Pupils (Ramasamy & Puteh, 2019)
This study examines the effectiveness of bar models in solving higher-order thinking skills (HOTs) math problems among Year 4 students. A pre-test and post-test analysis revealed that students using bar models demonstrated improved problem-solving skills and conceptual understanding, supporting the bar method as a powerful tool in math mastery.
2. The Introduction of the Singapore Bar Model in Year 1 Problem Solving: A Personal Reflection (Hofer, 2015)
This study explores the use of the Singapore Bar Model in Year 1 classrooms. Findings indicate that using the bar method enhances students' ability to link addition and subtraction concepts, improving their understanding of math topics. The study highlights the importance of combining pictorial representations with concrete materials for deeper learning.
3. Technology-Enabled Pedagogy to Bridge Bar Diagrams to Letter-Symbolic Algebra (Looi et al., 2007)
This research explores how bar diagrams can help students transition from arithmetic to algebra. A technology-enabled intervention was introduced to facilitate the bridging process, demonstrating that bar models improve students' ability to visualize mathematical relationships and support the acquisition of key algebraic skills.
4. The Effectiveness of Bar Model to Enhance HOTS in Length Word Problems (Karim & Puteh, 2021)
This study focuses on the application of bar models in solving length-related word problems. Results show significant improvements in students' problem-solving abilities when bar models were used as part of the CPA (Concrete-Pictorial-Abstract) approach in math education.
5. Determining the Effect of Bar Model Technique on Students’ Mathematical Word Problem Solving Skills (Shah, 2023)
This experimental study examines the impact of bar modelling on primary students' ability to solve word problems. Results indicate that bar models significantly enhance problem-solving strategies, especially in complex multi-step questions, reinforcing their role in developing essential practice skills in math.
Bar models are pictorial representations using rectangles or bars to show known and unknown quantities in maths problems, where the size of the bars is proportional to the values they represent. Unlike other visual tools, they don't provide direct answers but guide learners to understand the relationships between numbers and determine which operations are needed to solve problems.
Teachers should start with concrete manipulatives like Cuisenaire rods before moving to pictorial bar representations, beginning with simple part-whole relationships in early years. The process should involve explicit teacher modelling first, followed by guided practice, before allowing independent work, ensuring students progress gradually from concrete experiences to abstract mathematical notation.
Bar models provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts, making them particularly effective for students who find traditional abstract number concepts challenging. They help develop number sense by revealing the underlying structure of problems and can engage reluctant learners, fostering a genuine interest in mathematics through visual problem-solving approaches.
Comparison bar models are ideal for problems involving comparing quantities, whilst fraction bar models specifically help students understand fractional concepts and relationships. Bar model multiplication techniques work well for visualising multiplication equations, and the models can be extended to more complex topics like ratios and volume once students have mastered the basic concepts.
The most critical mistake is choosing the wrong type of bar model for a specific problem, which can actually make problem-solving more difficult rather than easier. Teachers should ensure they model the complete solution process first, allowing students to focus on understanding how the model demonstrates the solution rather than searching for the answer independently.
Bar models can start as early as Kindergarten using simple tools like Cuisenaire rods for basic part-whole relationships, with more formal bar models introduced in Year 1. As students progress through Years 4-6, bar models become particularly valuable for tackling complex topics like ratios and fractions that typically cause confusion at these levels.
Bar models serve as the crucial pictorial stage in the Concrete, Pictorial, Abstract (CPA) teaching sequence, helping students move from physical manipulatives to visual representations before reaching abstract notation. This systematic progression builds students' number sense and problem-solving skills whilst ensuring struggling learners aren't left behind during the critical transition to abstract mathematical concepts.
Mathematics can often seem daunting, but visual tools like bar models can transform the way students understand numbers. By translating complex problems into easily digestible visuals, these models provide clarity and facilitate deeper mathematical comprehension.
Bar models serve as powerful representations of mathematical concepts, allowing learners to visualize relationships between numbers. They are particularly significant in helping students grasp operations like addition, subtraction, multiplication, and division through concrete illustrations.
This article will explore the importance of bar models in math education, effective strategies for introducing them to students, common misconceptions to address, and their real-world applications. By mastering bar models, both educators and students can enhance their mathematical skills and foster a long-lasting understanding of the subject.
Bar models are crucial because they provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts. They help students visualize relationships between numbers and understand operations like addition, subtraction, multiplication, and division more deeply. This visual approach is particularly effective for students who struggle with traditional abstract number concepts.

Bar models are powerful tools in math education, offering visual representations that enhance a student's conceptual understanding. They serve as a bridge, connecting concrete objects with abstract mathematical concepts. By doing so, they help students grasp math operations like addition, subtraction, multiplication, and division more deeply.
Bar models come in various types, such as comparison models and fraction bar models, catering to different mathematical concepts and operations. These pictorial diagrams enable students to visualize complex problems and compare different quantities through bar model examples.

| Bar Model Types | Usage |
|---|---|
| Comparison Bar Models | Used for comparing quantities |
| Fraction Bar Models | Helps in understanding fractions |
| Bar Model Multiplication | Visualizes multiplication equations |
In conclusion, bar modelling is a versatile tool that can significantly impact pupils' understanding, boosting their confidence in math.

Bar models are visual representations using rectangles to help solve arithmetic problems. They are part of the concrete, pictorial, abstract (CPA) teaching method, which aids understanding and mastery of math concepts. Bar models help students visualize relationships in a problem and determine needed operations. They do not provide answers but guide learners on the necessary calculations.
Bar models are pictorial representations that use rectangles or bars to show known and unknown quantities in math problems. They are commonly used for addition, subtraction, multiplication, and division. The size of the bars is proportional to the values they represent, making it easy to see the relationships between numbers. The bar model technique fits with the CPA approach, emphasizing visual learning before moving to abstract math notation.
Bar modelling is a powerful tool for solving word problems. It helps students visualize complex calculations and understand math concepts better. Once mastered, bar modelling can be used for various topics like ratios, volume, and fractions. It aids in creating a strong logical foundation. By using bar models across the curriculum, students can see links between different math areas, deepening their understanding.

| Bar Model Benefits | Description |
|---|---|
| Visual Problem Solving | Converts word problems into visual models |
| Enhances Understanding | Allows better grasp of complex math concepts |
| Encourages Application | Builds a framework for applying knowledge to new topics |
Students develop a stable framework for math by engaging with bar models, increasing their overall confidence and fluency.
Start by using concrete manipulatives before moving to pictorial bar representations, following the concrete-pictorial-abstract (CPA) approach. Begin with simple part-whole relationships and gradually progress to more complex problems involving multiple operations. Model the process explicitly first, then provide guided practice before allowing independent work.
Bar models are powerful tools that help students visualize mathematical relationships. They aid in building a strong conceptual understanding by allowing students to see the connections between numbers. The journey with bar models can start early, like in Kindergarten, with simple tools like Cuisenaire rods. As students progress to 1st grade, they can tackle more formal bar models. Teachers should first present the complete solution. This lets students focus on how the model demonstrates the solution rather than searching for the answer. Choosing the right type of bar model is crucial. Using an incorrect model can make problem-solving more difficult. The bar model technique is key in moving from concrete experiences to abstract thinking. This builds a student's number sense and problem-solving skills.
The bar model method provides a structured way to teach math concepts. Students learn to visualize and understand how parts of a problem are related. Using the Concrete, Pictorial, Abstract (CPA) approach, teachers guide students from using real objects to drawing bar models. Eventually, students reach abstract notations. Encourage students to draw and share different representations of the same math problem. This practice enhances their understanding and problem-solving flexibility. A consistent teaching method for bar models across schools ensures that students receive a uniform learning experience. This leads to better learning outcomes. Introducing abstract representations alongside bar models helps students move from pictorial understanding to advanced reasoning in math.

Bar models act as visual aids that reinforce a student's understanding of math concepts. They illustrate the relationships between different quantities. Bar models are part of the CPA teaching sequence. They help students move from using physical objects to pictorial representations and finally to abstract notation. By visualizing the needed calculations, bar models allow students to solve problems without giving direct answers. This enhances their problem-solving skills. Hands-on tools like foam bars and magnetic dry wipe boards create engaging learning experiences. These tools make it easier for students to grasp mathematical concepts. Bar models are versatile. They are used for various math topics, such as addition, subtraction, multiplication, and division. This makes them integral to intervention strategies in education.
Bar models can be applied to solve word problems involving all four basic operations, fractions, ratios, and proportions. They are particularly effective for comparison problems, multi-step word problems, and algebraic thinking in elementary grades. These models help students organize information visually and identify the mathematical relationships within problems.
Bar models are powerful tools for visualizing mathematical concepts. They help children develop a conceptual understanding by using a concrete > pictorial > abstract (CPA) approach. This method moves from tangible objects to visual and finally to abstract ideas. Bar models can represent all major math operations: addition, subtraction, multiplication, and division. This versatility aids students in solving various types of problems, especially multi-step ones. Bar modeling provides a strong foundation for solving equations and understanding complex concepts.
In addition, bar models help students visualize number relationships through proportional rectangles. These visual representations guide students to focus on what calculations are necessary for solving problems. As they progress, students become more confident with addition. This includes not just basic sums but also complex concepts like fractions and ratios. Bar models align with the National Curriculum, helping young learners use concrete objects and pictorial diagrams to understand addition.
Bar models support subtraction by showing how it differs from and relates to addition. They offer part-part-whole and find-the-difference models. This helps students choose the right approach for each problem. Teachers guide students through these stages, moving from tangible objects to pictorial representations. Bar models in subtraction lead students to visualize problems clearly and choose the right calculations for solutions.
For multiplication, bar models showcase the relationship between quantities as repeated addition. Students see the multiplication process by repeating the same visual unit. This makes understanding the scale of their calculations easier. Bar models help students move from concrete examples to abstract math concepts. Mastering bar model multiplication equips students to tackle more complex math challenges.
In division, bar models focus on sharing. They visually represent how division works by showing quantities being divided. For example, if Mr. Smith divides a piece of wood using a bar model, each piece depicts a part of the division process. This visual strategy helps students grasp the concept of division and apply it to different problems. The proportional nature of bar models aids in understanding the relationship between quantities divided, fostering deeper comprehension.

The Singapore Bar Model Method is a visual problem-solving approach that uses rectangular bars to represent known and unknown quantities in mathematical problems. This method emphasizes understanding the relationships between parts and wholes before applying computational procedures. It has been widely adopted internationally due to its effectiveness in developing mathematical reasoning skills.
The Singapore Bar Model Method is a teaching technique that helps students understand mathematical concepts. Rooted in the theories of educators like Bruner, Dienes, and Bishop, it focuses on mastery in mathematics. This method uses bar models to bridge the gap between concrete objects and abstract ideas. Bar models help students move from using real items to grasping abstract math concepts.
Bar models are a type of pictorial representation. They show quantities and relationships in a structured manner. When students become skilled with bar models, they can use them for various math topics. These include ratio problems, fractions, and volume problems. By using bar models, students improve their problem-solving skills.
The Singapore Bar Model Method is versatile. It can be tailored to fit different math problems. This adaptability makes it a powerful tool for developing number sense and mathematical fluency.
Bar models serve as a visual aid to help children solve math problems. They use proportional rectangles to show different values. This enhances a child's understanding of math operations.
Benefits of Bar Models:
The Singapore Math Model, or bar modeling, makes learning math progressive and comprehensive. It is a valuable resource for teachers aiming to fill individual learning gaps in students.
The part-whole method uses bar models to show how smaller quantities (parts) combine to form a larger quantity (whole). Students draw bars divided into sections representing the known parts and identify what needs to be found. This visual representation helps students understand addition and subtraction as inverse operations and builds number sense.
The part-whole method is a powerful tool in the math classroom. It involves breaking numbers into parts that together form a whole. This method is great for addition and subtraction. By using proportional bars, students can visualize how parts relate to the whole. This visual representation aids in understanding complex math topics like fractions, measurement, algebra, and ratios.
Proportionality is key in this method. All the bar models must be roughly proportional to each other to accurately represent relationships. This technique is versatile and can be applied in various mathematical operations. When students get to see the part-whole models, they develop a clearer conceptual understanding of numerical relationships.

Bar models are pictorial representations that help illustrate math concepts. They use rectangles to represent numbers. This helps students see how to solve problems without giving away the answers. Bar models follow the concrete-pictorial-abstract (CPA) teaching sequence. This means students start with real objects, move to pictures, and then to abstract concepts.
Bar models are suitable for all four basic math operations: addition, subtraction, multiplication, and division. This makes them very versatile tools for learning. They can enhance a student's ability to visualize number relationships in a problem, fostering deeper understanding. These models are especially helpful in education for reinforcing concepts. They benefit students during catch-up sessions and align well with curriculum objectives for Key Stages 1 and 2.
Teachers often rush to abstract representations without sufficient concrete and pictorial practice, causing student confusion. Another common mistake is using bar models for every type of problem, even when other strategies might be more appropriate. Additionally, failing to explicitly teach when and why to use specific bar model types can lead to procedural errors rather than conceptual understanding.
Bar modelling is a powerful tool in teaching mathematical concepts. However, several common mistakes can hinder its effectiveness.
Misunderstandings about bar models can arise if not addressed early. Here are some misconceptions teachers should avoid:
To maximize the benefits of bar modelling, consider these instructional tips:
By avoiding common mistakes, addressing misconceptions, and following effective teaching strategies, educators can enhance the impact of bar modelling in math lessons. This ensures a better conceptual understanding among students.

Effective practice examples start with simple comparison problems like 'Tom has 8 stickers, Jerry has 3 more than Tom, how many does Jerry have?' Progress to multi-step problems involving different operations and real-world contexts that students can relate to. Include both part-whole and comparison model types to build comprehensive problem-solving skills.
Bar modelling is a powerful tool in math lessons. It helps children understand various math operations. By using visual and pictorial representations, students can grasp complex problems. These methods are especially useful for teaching addition, subtraction, multiplication, and division. They align with the concrete > pictorial > abstract (CPA) approach, which guides students from using concrete objects to understanding abstract ideas.
To teach addition, bar models can show students how to combine quantities. For instance, if you have 6 red pencils and 4 yellow pencils, a bar model can help visualize the total number of pencils. By drawing rectangles to represent each quantity, learners can better understand what they are adding. Teachers often use worksheets that gradually increase in difficulty. This helps students solidify their understanding before creating their own problems. Bar models help connect concrete resources to abstract calculations in addition.
Subtraction can be tricky, but bar models simplify it. Consider a problem where you compare how many more football cards one person has than another. With a bar model, students can see the difference as a space between two bars. This visual representation makes it easier to find unknown quantities. Using tools like Base 10 blocks alongside bar models helps reinforce subtraction concepts. This method encourages a deep conceptual understanding and helps students move from hands-on learning to abstract problem-solving.
For multiplication, bar models show grouped sets. Imagine solving a problem where you need to multiply 4 sets of 3. A bar model illustrates this by repeating a block of 3 four times. This visualization helps students understand that multiplication is repeated addition. Complex word problems become easier as students see the operation unfold visually. By linking abstract calculations with concrete images, bar models enable a better grasp of multiplication.
Bar models are also effective for division. They represent division as sharing an amount into equal parts. For example, if Mr. Smith cuts a 36 cm piece of wood into 6 equal pieces, a bar model shows each piece as 6 cm long. By visualizing these equal shares, students can better understand division problems. This approach clarifies how larger quantities divide into smaller, equal parts. By using bar models, learners can move from concrete understanding to abstract representations in division.
These practical examples demonstrate how bar modelling resources impact pupils' learning. They fill individual learning gaps and enhance conceptual understanding in elementary math education.
Bar models help students solve everyday problems involving money, measurements, time, and quantities in cooking or shopping scenarios. They can model budget allocation, ingredient ratios in recipes, or distance and time relationships in travel problems. These applications demonstrate the practical value of mathematical thinking beyond the classroom.
Bar models are a powerful visual tool in math. They help individuals tackle various mathematical concepts without jumping straight into complex calculations. By using proportional rectangles, bar models aid in visualizing problem-solving operations such as addition, subtraction, multiplication, and division. This visual strategy is especially beneficial for understanding word problems and identifying the necessary operations to solve them. As students engage with bar models, they progress through activities of increasing complexity. This allows them to master more advanced topics, like fractions and equations. Overall, bar models enhance reasoning skills and promote problem-solving prowess.
Bar models serve as a bridge between abstract math and the real world. They help students grasp mathematical concepts and apply them in practical situations. When learners use bar models, they can visualize the relationships between problem elements. This makes it easier to perform operations like addition, subtraction, multiplication, and division. By fostering conceptual understanding, children develop a stronger number sense and fluency in math. This new skill set enables them to tackle everyday challenges with confidence, and to use mathematical skills in real-life scenarios efficiently.
The significance of bar models extends beyond the classroom. These versatile tools not only help students tackle math problems but also enhance individual learning experiences. By offering a tangible way to connect experiences with abstract reasoning, bar models lay a robust foundation in math. Their simplicity, requiring only basic materials like pencils and paper, makes them accessible resources for students in test settings. Moreover, by aiding in the conceptual understanding of math operations, bar models equip children with skills that apply to real-world contexts and other academic subjects. This approach to learning prepares students for lifelong success in any mathematical endeavor they face.

The most effective strategy is following the concrete-pictorial-abstract progression, ensuring students master each stage before advancing. Use think-alouds to model the decision-making process when choosing which type of bar model to use. Provide regular opportunities for students to explain their thinking and justify their choice of representation.
The bar model is a versatile tool that acts as a visual representation to help students understand mathematical concepts. It doesn't solve problems directly but instead reveals the mathematical structure, enhancing problem-solving skills. The bar model method is a core part of the Singapore Math approach, helping students visualize and tackle problems, from simple operations to complex word problems.
Engaging students in math can be transformative, especially when using bar models. These visual representations make complex mathematical concepts easier to understand. They help students see math problems as pictorial diagrams, allowing them to grasp abstract ideas more readily. This builds confidence and can spark a love for math in even the most reluctant learners.
One-on-one tutoring programs personalized to each student’s needs can further enhance learning. Such programs help address individual learning gaps and provide targeted support. Worksheets that incorporate bar models serve as valuable resources in these sessions. They offer structured opportunities to explore various math operations and form a solid conceptual understanding.
To cater to diverse learning styles, differentiated worksheets can be introduced. These concrete resources allow students to explore math at their own pace, enhancing engagement and participation. Here's a quick list of how bar models impact learning:
In sum, bar modelling is a versatile tool that can boost student confidence and interest in math, providing elementary math teachers with effective ways to enhance their teaching.

Research consistently shows that bar models improve student performance in problem-solving and mathematical reasoning, particularly for students who struggle with traditional methods. Studies indicate that students who use bar models demonstrate better understanding of mathematical relationships and transfer skills to new problem types. The visual approach has been shown to reduce cognitive load and increase engagement across diverse learner populations.
These studies highlight the effectiveness of bar modelling in enhancing students’ problem-solving skills, mathematical reasoning, and ability to transition to more abstract mathematical concepts.
1. The Effectiveness of Bar Model to Enhance HOTs in Mathematics for Year 4 Pupils (Ramasamy & Puteh, 2019)
This study examines the effectiveness of bar models in solving higher-order thinking skills (HOTs) math problems among Year 4 students. A pre-test and post-test analysis revealed that students using bar models demonstrated improved problem-solving skills and conceptual understanding, supporting the bar method as a powerful tool in math mastery.
2. The Introduction of the Singapore Bar Model in Year 1 Problem Solving: A Personal Reflection (Hofer, 2015)
This study explores the use of the Singapore Bar Model in Year 1 classrooms. Findings indicate that using the bar method enhances students' ability to link addition and subtraction concepts, improving their understanding of math topics. The study highlights the importance of combining pictorial representations with concrete materials for deeper learning.
3. Technology-Enabled Pedagogy to Bridge Bar Diagrams to Letter-Symbolic Algebra (Looi et al., 2007)
This research explores how bar diagrams can help students transition from arithmetic to algebra. A technology-enabled intervention was introduced to facilitate the bridging process, demonstrating that bar models improve students' ability to visualize mathematical relationships and support the acquisition of key algebraic skills.
4. The Effectiveness of Bar Model to Enhance HOTS in Length Word Problems (Karim & Puteh, 2021)
This study focuses on the application of bar models in solving length-related word problems. Results show significant improvements in students' problem-solving abilities when bar models were used as part of the CPA (Concrete-Pictorial-Abstract) approach in math education.
5. Determining the Effect of Bar Model Technique on Students’ Mathematical Word Problem Solving Skills (Shah, 2023)
This experimental study examines the impact of bar modelling on primary students' ability to solve word problems. Results indicate that bar models significantly enhance problem-solving strategies, especially in complex multi-step questions, reinforcing their role in developing essential practice skills in math.
Bar models are pictorial representations using rectangles or bars to show known and unknown quantities in maths problems, where the size of the bars is proportional to the values they represent. Unlike other visual tools, they don't provide direct answers but guide learners to understand the relationships between numbers and determine which operations are needed to solve problems.
Teachers should start with concrete manipulatives like Cuisenaire rods before moving to pictorial bar representations, beginning with simple part-whole relationships in early years. The process should involve explicit teacher modelling first, followed by guided practice, before allowing independent work, ensuring students progress gradually from concrete experiences to abstract mathematical notation.
Bar models provide visual representations that bridge the gap between concrete objects and abstract mathematical concepts, making them particularly effective for students who find traditional abstract number concepts challenging. They help develop number sense by revealing the underlying structure of problems and can engage reluctant learners, fostering a genuine interest in mathematics through visual problem-solving approaches.
Comparison bar models are ideal for problems involving comparing quantities, whilst fraction bar models specifically help students understand fractional concepts and relationships. Bar model multiplication techniques work well for visualising multiplication equations, and the models can be extended to more complex topics like ratios and volume once students have mastered the basic concepts.
The most critical mistake is choosing the wrong type of bar model for a specific problem, which can actually make problem-solving more difficult rather than easier. Teachers should ensure they model the complete solution process first, allowing students to focus on understanding how the model demonstrates the solution rather than searching for the answer independently.
Bar models can start as early as Kindergarten using simple tools like Cuisenaire rods for basic part-whole relationships, with more formal bar models introduced in Year 1. As students progress through Years 4-6, bar models become particularly valuable for tackling complex topics like ratios and fractions that typically cause confusion at these levels.
Bar models serve as the crucial pictorial stage in the Concrete, Pictorial, Abstract (CPA) teaching sequence, helping students move from physical manipulatives to visual representations before reaching abstract notation. This systematic progression builds students' number sense and problem-solving skills whilst ensuring struggling learners aren't left behind during the critical transition to abstract mathematical concepts.